[핸즈온 머신러닝] 규제

• 이전까지 선형 모델의 비용 함수는 RSS를 최소화하는, 즉 실제 값과 예측 값의 차이를 최소화하는 것만 고려
• 그 결과 학습 데이터에 과대적합되어 회귀 계수가 쉽게 커져 변동성이 오히려 심해져 테스트 데이터셋에서 예측 성능이 저하됨

• alpha : 학습 데이터 적합 정도와 회귀 계수 값 크기 제어하는 튜닝 파라미터
• alpha ↑ : 회귀 계수 W의 값 작게 해 과적합 개선

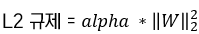
: 릿지(Ridge) 회귀

 

: 라쏘(Lasso) 회귀

 

릿지 회귀

• 규제항으로 회귀계수 제곱 합 대입
• α가 0이면 선형 회귀
• α가 매우 크면 모든 가중치는 거의 0에 가까워지고 결국 데이터의 평균 지나는 수평선이 됨

 

• StandardScaler와 같은 라이브러리를 이용해 데이터 스케일 맞춰야 함
• α를 증가시킬수록 직선에 가까워짐

 

릿지 회귀의 정규방정식

확률적 경사 하강법

 

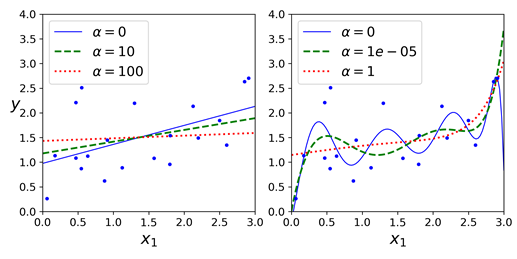
라쏘 회귀

• 규제항으로 회귀계수의 절댓값 합 대입
• 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거
• 적절한 피처만 회귀에 포함시키는 특성 선택을 하고 희소 모델 만듦

 

기하학적 이해

릿지 회귀

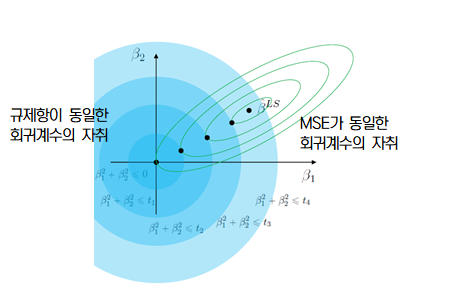
• $β^{LS}$ : 일반 선형 회귀 모델 결과, MSE가 최소가 되는 지점. 멀어질수록 MSE가 작아짐
• 원의 반지름이 작아질수록 규제항이 감소하고 제약이 커짐 = α가 클수록 규제항이 작아짐
• 규제항을 통해 제약을 가했다면 그 제약을 만족하면서 MSE가 최소인 지점에 해당하는 회귀계수를 찾게 됨

라쏘 회귀

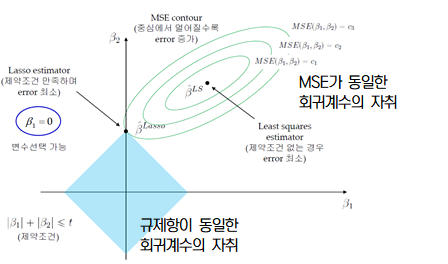
• 파란색 마름모 꼴의 제약 범위 내에 MSE가 최소인 점은 $β_2$ 축 위의 검정색 점, 즉 $β_1$=0인 지점 = 대응하는 독립변수 $x_1$이 예측에 중요하지 않음
• 0에서 미분이 불가능하므로 서브그레디언트 벡터를 사용해 경사 하강법 적용 가능

엘라스틱넷

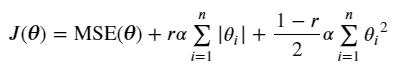
• $r$ : 혼합 비율
• $r$=0이면 릿지 회귀, $r$=1이면 라쏘 회귀

• l1_ratio = $r$ (혼합 비율)

 

규제 모델 비교