A spatial scan statistic for zero-inflated Poisson process

pdf

github

---

Introduction

1. Spatial scan statistic

- 주어진 지역 내에서 특정 사건이 유의하게 발생하는 소단위 지역을 감지하는 데 사용되는 통계량 (Kulldorff, 1997)
- 이러한 count data는 대부분 포아송 모형으로 적합하지만, 실제 데이터에서 값이 0인 경우가 많으면 평균과 분산이 동일하다는 포아송의 기본 가정을 위배함

 

2. Zero-inflated data

- 실제 관측치가 0인 경우 (sampling zero) + 측정이 불가능해 0으로 간주된 경우 (structural zero)
   = zero-inflation
- zero-inflated data에 포아송 모형을 적합할 경우, 유의한 클러스터를 찾아내는 성능이 떨어진다는 연구 결과

목표 : zero-inflated data에서 유의한 클러스터를 감지하는 데 용이한 Scan-ZIP 통계량 소개

Methodology

Scan-Poisson

1. Assumptions

- 방법론을 설명하기에 앞서 몇가지 notation을 정의하자

- $k$개의 지역
- $x_i$ : $i$번째 지역의 사건 발생 수
- $n_i$ : $i$번째 지역의 총 위험 인구
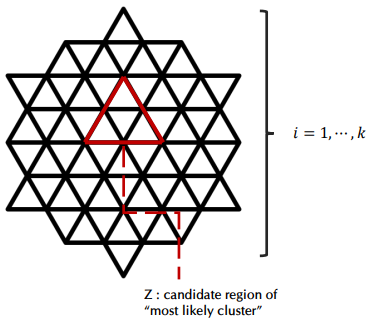
- $Z$ : $k$개의 지역 중 일부 잠재 지역
- $\bar{Z}$ : $Z$에 속하지 않는 지역
- $\theta _Z$ : $Z$에 속하는 지역의 상대 위험도
- $\theta _0$ : $Z$에 속하지 않는 지역의 상대 위험도

- 단 이때 $Z$에 속하는 지역의 $\theta_i$와 속하지 않는 지역의 $\theta_i$는 모두 같다.

- $x_Z = \sum_{i \in Z} x_i, x_{\bar{Z}} = \sum_{i \in \bar{Z}} x_i, x=x_Z + x_{\bar{Z}}$

- $n_{\bar{Z}} = \sum_{i \in \bar{Z}} n_i, n_{\bar{Z}} = \sum_{i \in \bar{Z}} n_i$

 

2. Hypothesis test

- $H_0 : \theta_Z = \theta_0$ vs. $H_a : \theta_z > \theta_0, Z \in \mathbb{Z}$
- 이때 $H_0$가 reject된다는 것은 $Z$에 상대 위험도가 높은 지역이 적어도 하나 포함된다는 의미

 

3. Scan-Poisson statistic

 

Scan-ZIP

1. Assumptions

- $X_i \sim ZIP(p, n_i\theta_i), p$ : 각 지역이 structural zero를 가질 확률 ($X_i$ are independent)

 

2. ZIP distribution

 

3. Hypothesis test

- $H_0 : \theta_Z = \theta_0$ vs. $H_a : \theta_z > \theta_0, Z \in \mathbb{Z}$
- 이때 $H_0$가 reject된다는 것은 $Z$에 상대 위험도가 높은 지역이 적어도 하나 포함된다는 의미

 

4. Scan-ZIP statistic

 

5. EM algorithm

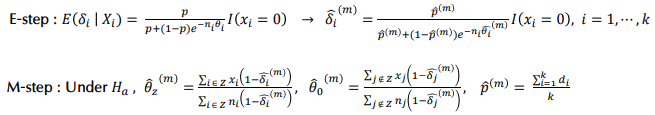
- 해당 지역의 데이터가 structural zero인지 모를 경우에는 EM 알고리즘을 이용해 $\delta$를 추정함

 

Simulation

Simulation design

- 총 9개의 시나리오

- 203개의 육각형 셀로 구성, 인접한 셀 사이의 거리는 모두 동일

- 회색 : true cluster, X : structural zero region

- $n$ : 각 셀에 할당된 인구 (=1,000)

- $N$ : 전체 인구 (=203,000)

- $C$ : 전체 사건 수 (=507, 전체 인구의 0.25%)

- $x_i \sim multinomial(C, \theta_1, ..., \theta_{203})$ : 각 셀의 사건 수

- $\sum _{i=1} ^k \delta_i = 15$ : structural region의 총 개수 = 15

 

Algorithms

Step1) Generate true cluster

• $x_i \sim multinomial(C, \theta_1, ..., \theta_{203})$이므로 relative risk에 비례하는 확률로 사건 수 할당
• relative risk : standard binomial test 기준 0.999의 검정력을 갖도록 지정

Step2) Find the most likely cluster

1. $z_i ^{(j)}$ : $i$ 지역에서 $j$번째로 가까운 지역들의 집합
2. $j=1,...,k$, $z_i ^{(j)}$에 속하는 인구가 총 인구의 절반을 넘지 않을 때까지 $LR(z_i ^{(j)})$ 계산
3. $i=1,...,k$에 대해 1.~2. 반복
4. LRs 중 가장 큰 값에 대응되는 클러스터 = “most likely cluster”

Step3) Obtain critical value ($\lambda ^*$)

• 기각역을 정의하기 위해 Monte Carlo 진행

1. 귀무가설 하에서 true cluster 생성
2. Scan-Poisson, Scan-ZIP, Scan-ZIP+EM → $\lambda$ 계산
3. 1.~2.를 B=1000번 반복
4. $\alpha=0.05$, $100(1-\alpha)$% of $\lambda = \lambda^*$

Step4) Get Power, Sensitivity, PPV

• Step 1~2를 N=2000번 반복

 

Result

Scenario A, B, C, D

• structural zero region 모두 동일, true cluster region 모두 다른 상황
• circular window로 true cluster를 탐색하기 때문에 true cluster가 원형의 형태가 아닌 불규칙한 형태를 가지고 있는 Scenario D가 다른 경우에 비해 성능이 낮음
• true cluster 내에 structural zero region이 많을 수록 성능 저하
  • C > B > A
• Scan-ZIP > Scan-ZIP+EM >> Scan-Poisson

Scenario A0, A1, A2, A3, A4

• true cluster region 모두 동일, true cluster 내 structural zero region 개수 다른 상황
• true cluster 내 structural zero region 개수가 많을수록 성능 저하
  • A1 > A2 > A3 > A4
• 대조군인 A0는 structural zero region이 없는 상태임에도 EM으로 추정한 Scan-ZIP 모델이 기존 Scan-Poisson과 큰 차이를 보이지 않음

⇒ Structural zero 유무에 관계없이 Scan-ZIP 모델이 더 범용적으로 쓰일 수 있음